Word2vec Tutorial

word2vec 是由 Tomas Mikolov 等人發展出來，把詞轉換成向量的一種演算法，使用三層架構的神經網路，輸入層與輸出層大小都是訓練文本的詞數，中間層大小就是想要壓縮的向量大小，平常神經網路訓練完我們都是想要最終的輸出結果，但 word2vec 訓練完的權重才是我們想要的東西，為什麼是這樣呢？我接下來直接用例子來解釋，這篇教學會講到數學推導和實作，程式碼在這。

Introduction⌗

假如現在文本只有 2 行 5 種詞，如下

狗會跑
魚會游

每個詞都想要壓縮成 3 維的向量，那模型的架構就會長這樣

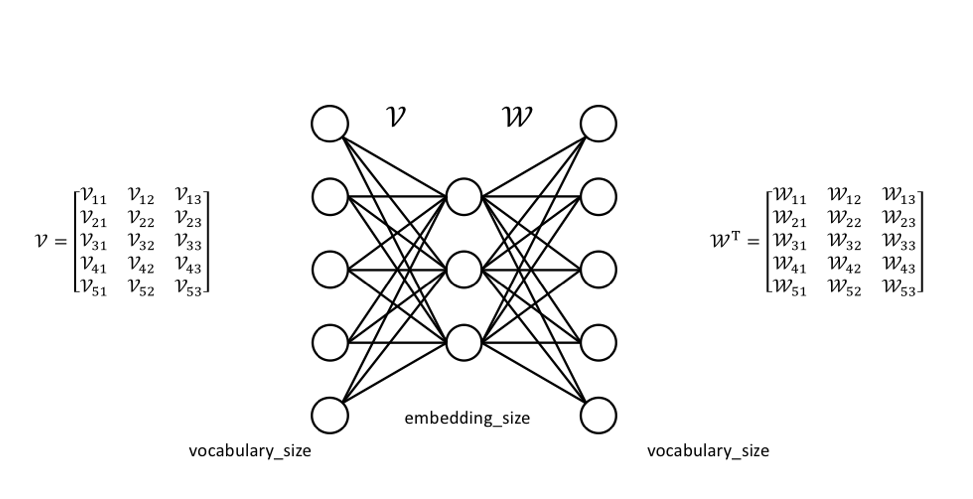
權重 v 和 w 初始值隨機給，我們拿到文本後就可以把每個詞用 one-hot encoding 的方式轉換

$狗= [\begin{matrix} 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{matrix}] 會= [\begin{matrix} 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{matrix}] 跑= [\begin{matrix} 0 \\ 0 \\ 1 \\ 0 \\ 0 \end{matrix}] 魚= [\begin{matrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \end{matrix}] 游= [\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{matrix}]$

這時如果我們要對「狗」這個詞進行訓練，就會可以知道以 v 這個權重來說，會需要更新的只有 $[\begin{matrix} v_{11} & v_{12} & v_{13} \end{matrix}]$

$[\begin{matrix} 1 & 0 & 0 & 0 & 0 \end{matrix}] [\begin{matrix} v_{11} & v_{12} & v_{13} \\ v_{21} & v_{22} & v_{23} \\ v_{31} & v_{32} & v_{33} \\ v_{41} & v_{42} & v_{43} \\ v_{51} & v_{52} & v_{53} \end{matrix}] = [\begin{matrix} v_{11} & v_{12} & v_{13} \end{matrix}]$

至於 w 那邊也是一樣，所以實際上最後訓練出來的權重 v 和 w 都可以用，只是大部分習慣都只拿 v 當最後的壓縮向量。

Intuition⌗

在神經網路中最重要的就是 loss function 了，word2vec 的 loss function 定義為

$J = - \log σ (v_{I}^{T} w_{p o s}) - \sum_{n e g} E_{w_{n e g} \sim P_{n} (I)} [\log σ (- v_{I}^{T} w_{n e g})]$

$σ$ 是 sigmoid function， $v_{I}$ 代表 input word 的權重向量， $w_{p o s}$ 代表 positive sample 的權重向量， $w_{n e g}$ 代表 negative sample 的權重向量， $P_{n}$ 代表一個分佈，negative sample 從這個分佈被出抽出來。

那什麼是 positive sample 和 negative sample？ word2vec 是一個詞袋模型，可以想像跟目標詞在同一個袋子裡的就是 positive sample，不在袋子裡的就是 negative sample，是否在袋子裡用 window size 去定義，假如 window size 是 1，就代表目標詞上下一個詞是在同一個袋子裡，例如「狗會跑」這句，對「狗」來說同一個袋子裡的就有「會」這個詞。

那為什麼 loss function 要這樣定義呢？就要來看看什麼情況下 loss function 會趨近於 0，我們都知道 log0 等於負無限大，log1 等於 0，sigmoid function 又是個介於 0 到 1 之間的函數，所以代表 $J$ 要趨近於 0 就代表， $σ (v_{I}^{T} w_{p o s})$ 和 $σ (- v_{I}^{T} w_{n e g})$ 都要趨近於 1，這樣就代表 $v_{I}^{T} w_{p o s}$ 要趨近於無限大， $v_{I}^{T} w_{n e g}$ 要趨近於負無限大，所以 input word 的權重向量要跟 positive sample 的權重向量內積越大越好，也就是角度要越小越好，跟 negative sample 的權重向量內積要越小越好，角度要越大越好。

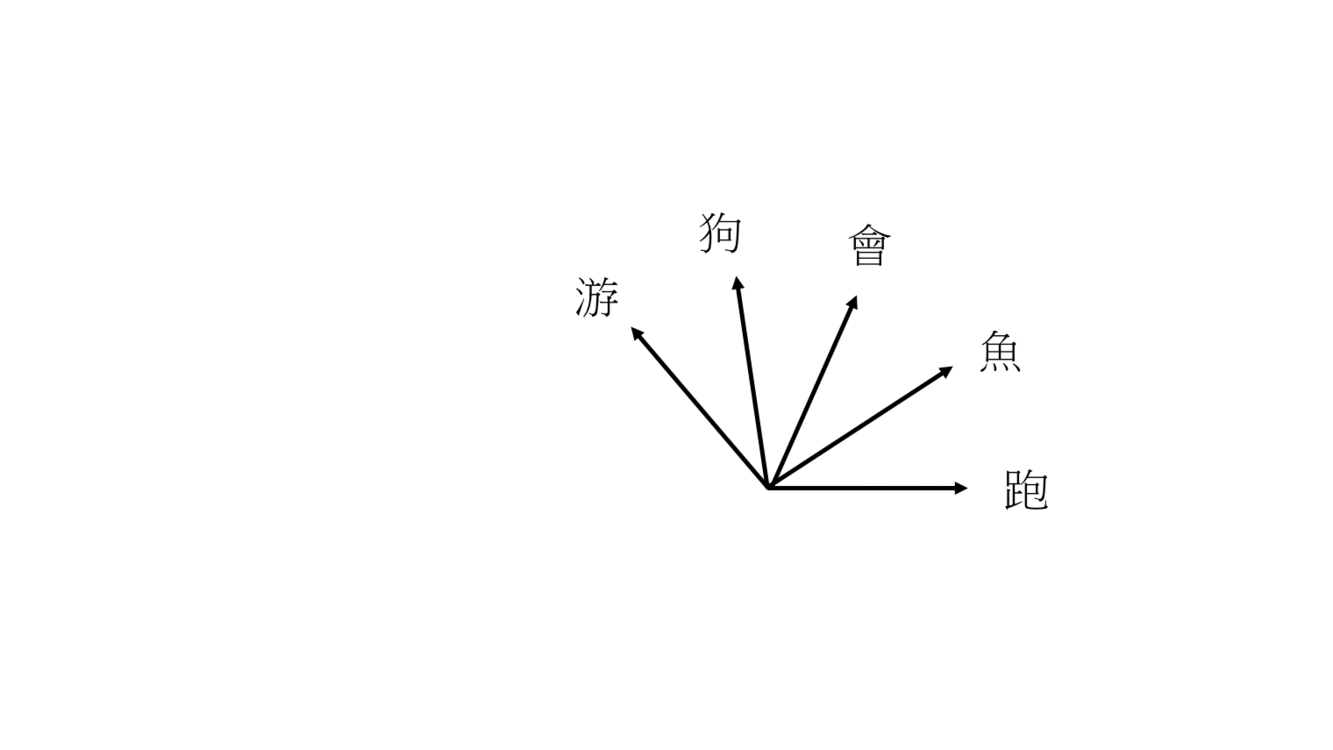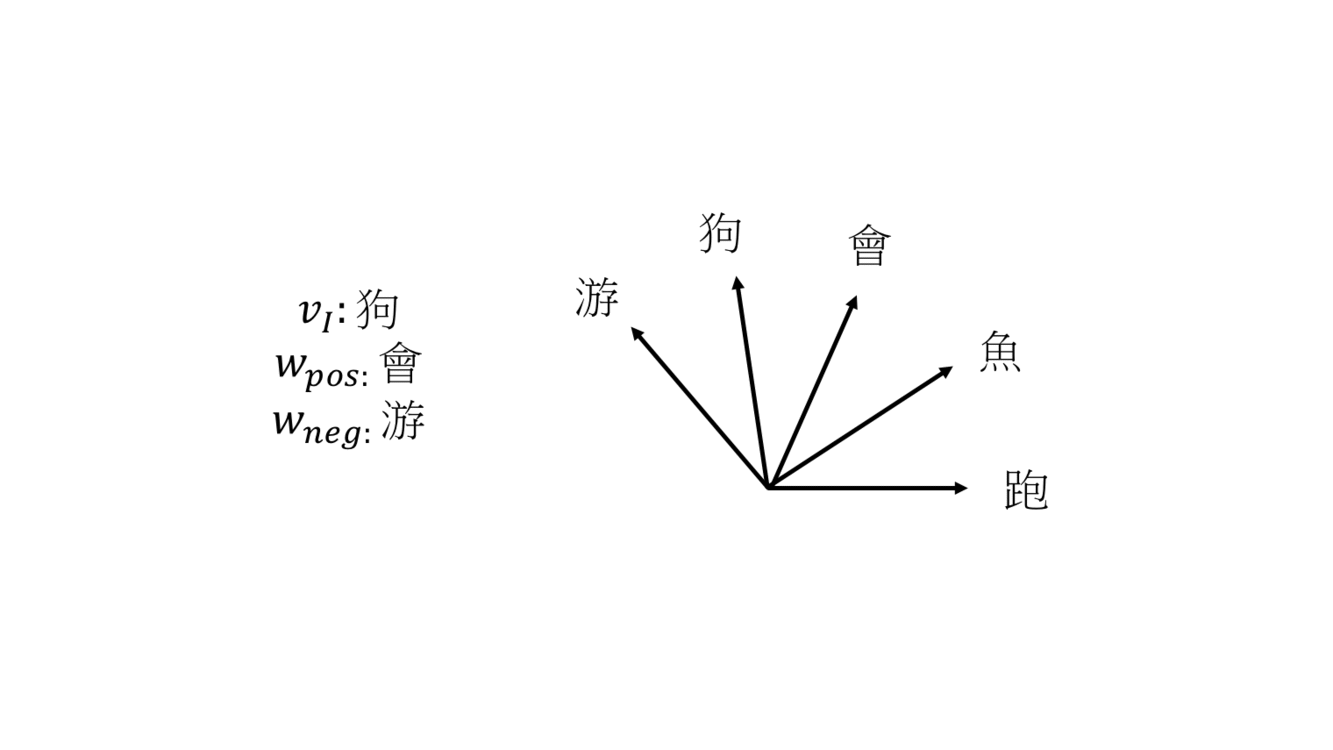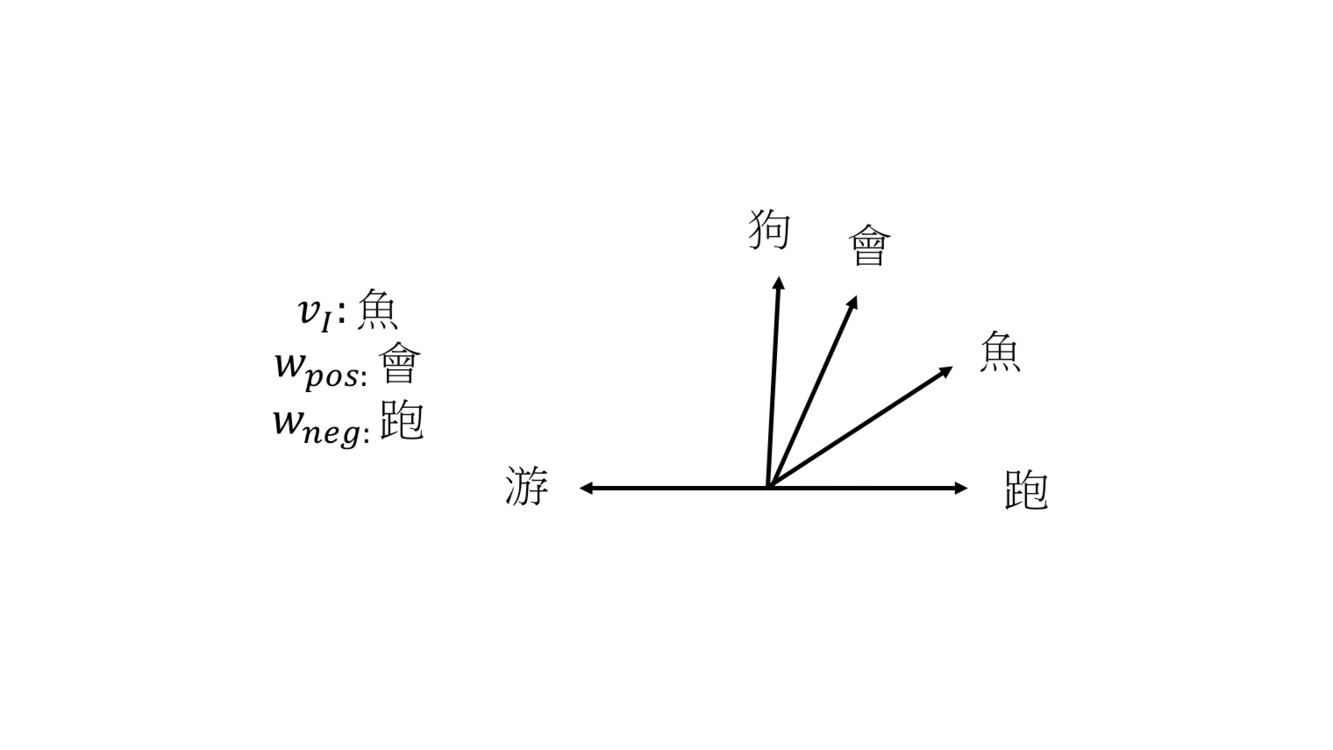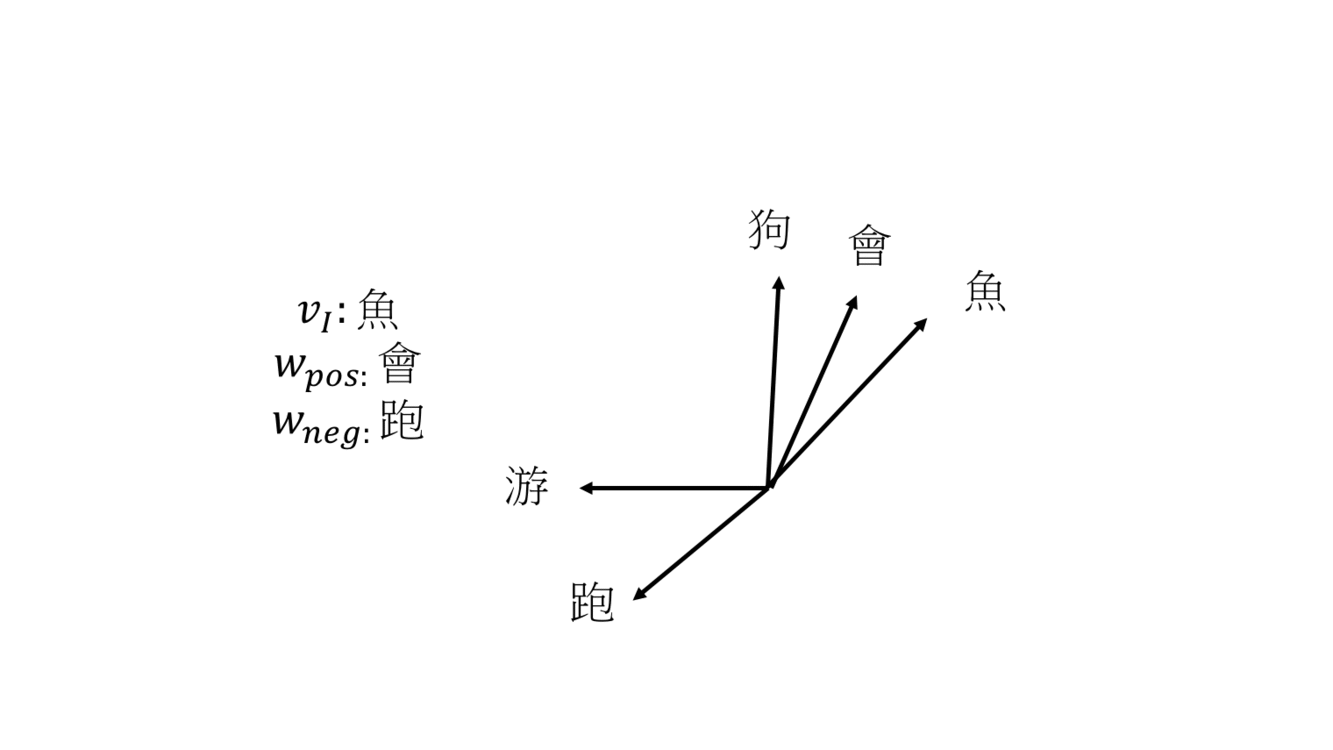
一開始 5 個詞的權重向量是隨機給的，第一輪要訓練的 input word 是「狗」，positive sample「會」，negative sample「游」，這時因為要讓 loss 變小所以，狗和會的權重向量角度拉近，狗和游的權重向量角度分開，第二輪 input word 是「魚」，positive sample「會」，negative sample「跑」，魚和會角度縮小，魚和跑角度變大，經過訓練會讓詞義相近的向量接近。

Backpropagation⌗

了解 loss function 就可以來算 gradient 更新權重了，為了方便後面推導，先定義一下

$v = [\begin{matrix} v_{11} & v_{12} & v_{13} \\ v_{21} & v_{22} & v_{23} \\ v_{31} & v_{32} & v_{33} \\ v_{41} & v_{42} & v_{43} \\ v_{51} & v_{52} & v_{53} \end{matrix}] = [\begin{matrix} v_{1} \\ v_{2} \\ v_{3} \\ v_{4} \\ v_{5} \end{matrix}]$

$w^{T} = [\begin{matrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ w_{31} & w_{32} & w_{33} \\ w_{41} & w_{42} & w_{43} \\ w_{51} & w_{52} & w_{53} \end{matrix}] = [\begin{matrix} w_{1} \\ w_{2} \\ w_{3} \\ w_{4} \\ w_{5} \end{matrix}]$

延續剛才的例子，第一輪 $v_{I}$ 、 $w_{p o s}$ 、 $w_{n e g}$ 分別是「狗」、「會」、「游」的權重向量，所以對於 positive 的部分要要更新的權重如下

$v_{1} \leftarrow v_{1} - η \nabla_{v_{1}} J$

$w_{2} \leftarrow w_{2} - η \nabla_{w_{2}} J$

對於 negative 的部分要更新的是

$v_{1} \leftarrow v_{1} - η \nabla_{v_{1}} J$

$w_{5} \leftarrow w_{5} - η \nabla_{w_{5}} J$

Positive⌗

先看 $v_{1} \leftarrow v_{1} - η \nabla_{v_{1}} J$ 這部分， $J$ 對 $v_{1}$ 的 gradient 可以寫成

$\nabla_{v_{1}} J = [\begin{matrix} \frac{\partial J}{\partial v_{11}} \\ \frac{\partial J}{\partial v_{12}} \\ \frac{\partial J}{\partial v_{13}} \end{matrix}]$

定義

$x_{12} = v_{1}^{T} w_{2}$

$J = - \log σ (x_{12})$

就可以把式子改寫一下

$\frac{\partial J}{\partial v_{11}} = \frac{d J}{d x_{12}} \frac{d x_{12}}{d v_{11}}$

$\frac{d J}{d x_{12}} = \frac{d - \log σ (x_{12})}{d x_{12}} = - \frac{1}{σ (x_{12})} σ (x_{12}) (1 - σ (x_{12})) = σ (x_{12}) - 1$

$\frac{d x_{12}}{d v_{11}} = \frac{d (v_{1}^{T} w_{2})}{d v_{11}} = \frac{d (v_{11} w_{21} + v_{12} w_{22} + v_{13} w_{23})}{d v_{11}} = w_{21}$

這時就可以代回去原本的

$\frac{\partial J}{\partial v_{11}} = (σ (x_{12}) - 1) w_{21} = (σ (v_{1}^{T} w_{2}) - 1) w_{21}$

$\nabla_{v_{1}} J = [\begin{matrix} \frac{\partial J}{\partial v_{11}} \\ \frac{\partial J}{\partial v_{12}} \\ \frac{\partial J}{\partial v_{13}} \end{matrix}] = [\begin{matrix} (σ (v_{1}^{T} w_{2}) - 1) w_{21} \\ (σ (v_{1}^{T} w_{2}) - 1) w_{22} \\ (σ (v_{1}^{T} w_{2}) - 1) w_{23} \end{matrix}] = (σ (v_{1}^{T} w_{2}) - 1) w_{2}$

最終得到

$v_{1} \leftarrow v_{1} - η (σ (v_{1}^{T} w_{2}) - 1) w_{2}$

至於 w 的部分也是一樣步驟，所以可以得到

$w_{2} \leftarrow w_{2} - η (σ (v_{1}^{T} w_{2}) - 1) v_{1}$

Negative⌗

negative 跟 positive 差別在於幾個小地方

$x_{15} = v_{1}^{T} w_{5}$

$J = - \log σ (- x_{15})$

所以

$\frac{d J}{d x_{15}} = \frac{d - \log σ (- x_{15})}{d x_{15}} = - \frac{1}{σ (- x_{15})} σ (- x_{15}) (1 - σ (- x_{15})) = 1 - σ (- x_{15}) = σ (x_{15})$

最終得到

$v_{1} \leftarrow v_{1} - η (σ (v_{1}^{T} w_{2}) - 0) w_{5}$

$w_{5} \leftarrow w_{5} - η (σ (v_{1}^{T} w_{5}) - 0) v_{1}$

Update weight⌗

回想一下剛才在 intuition 的部分有講到 $σ (v_{I}^{T} w_{p o s})$ 和 $σ (- v_{I}^{T} w_{n e g})$ 都要趨近於 1，也就是 $σ (v_{I}^{T} w_{p o s})$ 要趨近於 1， $σ (v_{I}^{T} w_{n e g})$ 要趨近於 0，對照剛才 update 的公式，有種跟目標差異多少就矯正回來的感覺。

Implementation⌗

有了前面的知識後我們就可以實際寫程式，跑跑看結果，很多教學文章都直接用 genism 這個已經寫好的模型來做實驗，但身為一個資工系學生還是想自己動手刻看看，所以我最後實作了兩個版本，一是自己刻的（很大部分參考 Mark 的 code），第二個版本是用 tensorflow ，由於 tensorflow 官方就有自己給 word2vec，所以我改動的部分就是讀資料的部分，兩個一起對照比較會更了解，code 可以直接到我的 github 看，這邊講解一些實作會遇到的細節。

Data⌗

中文訓練詞向量會遇到斷詞的麻煩，雖然現在都可以用 jiaba 這個斷詞工具來解決，但為了減少麻煩我就選用唐詩來當語料庫，我用別人已經整理好的資料 chinese-poetry 中唐詩的部分。

假如一個句子 秦川雄帝宅轉換成 index [149, 65, 199, 250, 345]，window_size 選擇 1，經過前處理後就會變成這樣，左是 input word，右是 positive sample。

[149, 65]  #秦 -> 川
[65, 149]  #川 -> 秦
[65, 199]  #川 -> 雄
[199, 65]  #雄 -> 川
[199, 250] #雄 -> 帝
[250, 199] #帝 -> 雄
[250, 345] #帝 -> 宅
[345, 250] #宅 -> 帝

Unigram distribution⌗

在選擇要用哪些詞當負樣本時要怎麼選？也就是公式中的 $P_{n}$ 是什麼？基本上設計這個分佈時希望詞被抽到的機率要跟這個詞出現的頻率有關，出現在文本中的頻率越高越高越有可能被抽到，Mikolov 他們在 paper 中給出一個公式

$P (w_{i}) = \frac{{f (w_{i})}^{3 / 4}}{\sum_{j = 0}^{n} ({f (w_{j})}^{3 / 4})}$

$f (w_{i})$ 代表 $w_{i}$ 這個詞出現的次數，那為什麼會有 3/4 次方這個東西？ paper 上面寫說是他們實驗出來覺得最好的結果，我們稱這個分佈為 unigram distribution，所以可以製造一個 unigram table，依照某個詞出現的次數乘以 0.75 次方，這就是他在 unigram table 出現的次數，最後就只要從這個 unigram table 隨機抽樣就好了，例如：有一個詞編號是 100，它出現在整個文本中 1000 次，所以 100 在 unigram table 就會出現 1000 ^ 0.75 = 177 次，實作如下

def build_unigram_table(word_dict):
  frq = map(lambda v: int(v**0.75), word_dict.values())
  t = [np.full(v, i, dtype=int) for i, v in enumerate(frq)] 

  return np.concatenate(t) # for negative sampling

至於要選幾個詞當 negative sample，paper 中建議如下

Our experiments indicate that values of k in the range 5–20 are useful for small training datasets, while for large datasets the k can be as small as 2–5.

Subsampling of frequent words⌗

英文中 “the”, “a”, “in”，中文中的「的」、「是」等等這種詞，其實在句子中並沒有辦法提供太多資訊但又常常出現，對訓練沒有太大幫助，所以就用一個機率來決定這個詞是否要被丟掉，公式如下

$P (w_{i}) = (\sqrt{\frac{z (w_{i})}{0.001}} + 1) \cdot \frac{0.001}{z (w_{i})}$

$z (w_{i})$ 代表 $w_{i}$ 這個詞出現的頻率，這裡的公式跟 paper 的並不一樣，因為我參考 Chris McCormick 的 blog 得知 Google 實作 word2vec 的 C code 裡面是這個公式，建議可以看看 Chris McCormick 的文章，他有探討為什麼這樣設計這個公式，我自己理解覺得這裡在做的事跟去掉 stop word 是一樣的概念。

z = word_dict[s[w]] / total_words
keeping_rate = (np.sqrt(z / 0.001) + 1) * (0.001 / z)
if keeping_rate < np.random.uniform(): continue # discard the word appears too frequently

Using tensorflow⌗

用 tensorflow 實作時 unigram distribution 和 backpropagation 都不用處理，參照 Google 給的 basic example，直接使用一個 loss function 稱為 tf.nn.nce_loss

loss = tf.reduce_mean(
    tf.nn.nce_loss(weights=nce_weights,
      biases=nce_biases,
      labels=train_labels,
      inputs=embed,
      num_sampled=num_sampled,
      num_classes=vocabulary_size)

解釋每個參數：

weights: 維度為 (vocabulary_size, hidden_layer_size)、初始化是隨機值的矩陣
biases: 維度為 (vocabulary_size, 1)、初始化是 0 的矩陣，因為 word2vec 沒有用到 biases
labels: 前處理後的資料，class -> label
inputs: 這次 batch 選中要訓練的詞的 weight
num_sampled: 要選幾個負樣本
num_classes: 文本中有幾個要被訓練的詞
num_true (default=1): 一次訓練時目標的類別有幾個
remove_accidental_hits (default=True): 初步理解是如果在負採樣時選到正樣本要不要丟掉，但根據 Google 給的文件感覺還有一些別的意義，目前還沒仔細研究
partition_strategy (default=‘mod’): 對 weights 查表的策略
name (default=‘nce_loss’): 給這個動作的名字，對 TensorBoard 有用
sampled_values (default=None): 要給他負採樣的樣本，如果是 None ，他會自己選擇 tf.nn.log_uniform_candidate_sampler 這個 sampler，他選擇負樣本的方式是

$P (c l a s s) = \frac{l o g (c l a s s + 2) - l o g (c l a s s + 1)}{l o g (n + 1)}$

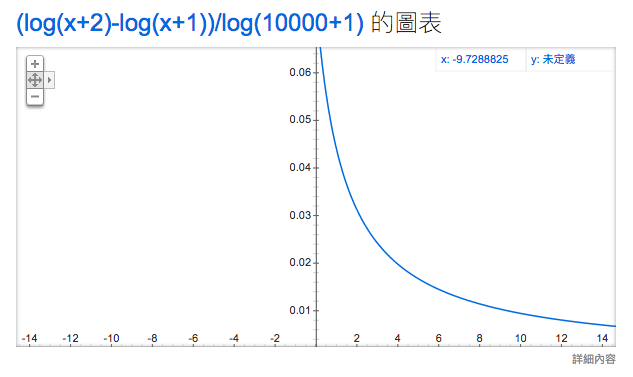
n 是 vocabulary_size，假設有個文本的 vocabulary_size 是 10000，可以在 Google 直接打 plot (log(x + 2) - log(x + 1)) / log(10000 + 1)，觀察知道如果他的 class 比較小就會比較容易被選到，所以在把詞轉換成 index 時，要依照出現次數排列，跟 unigram distribution 的方法不一樣，但都是越常出現越容易被選到的想法。

Result⌗

# from scratch               # tensorflow      
# spend: 53.94 min           # spend: 38.09 min 
                             
雲 1.0                       雲 1.0
嵐 0.818097894953            嵐 0.731922132211
緲 0.807170161919            霞 0.710187307407
烽 0.806751349354            烟 0.693668808384
烟 0.791932317029            雪 0.684637639979
靄 0.790464066718            虹 0.683235227787
-----                        -----
峰 1.0                       峰 1.0
峯 0.96521154438             峯 0.942029995583
層 0.869375215503            嶽 0.73387296403
巒 0.847521841138            嵋 0.732944525
巖 0.842055300736            巒 0.716149847575
巔 0.834164942036            巔 0.714281751101
-----                        -----
風 1.0                       風 1.0
飆 0.839413385589            吹 0.820511746298
涼 0.812897226871            飆 0.809179019451
凜 0.790959089145            逆 0.67986909613
颸 0.786966264664            颸 0.663089281948
暄 0.771490669881            涼 0.659044072466
-----                        -----
女 + 父 - 男                 女 + 父 - 男
母 0.765840473955            母 0.735594336365
婦 0.758031202523            子 0.729155945201
子 0.724152991944            伴 0.696736003898
伴 0.707958812532            彿 0.645417693955
阿 0.702062120972            阿 0.629788529922

Acknowledgments and references⌗

Mark Chang 的部落格幫助我很多，尤其是我大量參考推導公式與第三篇實作 code 的內容，非常推薦值得一讀
Chris McCormick 的部落格，講得非常簡潔明瞭，細節也解釋的非常棒，作者還有自己去 trace Google 他們釋出的 word2vec C code
- McCormick, C. (2016, April 19). Word2Vec Tutorial - The Skip-Gram Model. Retrieved from http://www.mccormickml.com
- McCormick, C. (2017, January 11). Word2Vec Tutorial Part 2 - Negative Sampling. Retrieved from http://www.mccormickml.com
Tensorflow 官方文件可以用這個當入門了解 word2vec 的概念
word2vec paper
- Mikolov, Tomas, et al. “Efficient estimation of word representations in vector space.” arXiv preprint arXiv:1301.3781 (2013).
- Mikolov, Tomas, et al. “Distributed representations of words and phrases and their compositionality.” Advances in neural information processing systems. 2013.
感謝 Aaron Chen 當我第一個讀者還幫我偵錯 🙏

Appendix⌗

$σ (x) = \frac{1}{1 - e^{- x}}$

$\frac{d σ (x)}{d x} = σ (x) (1 - σ (x))$

$σ (x) + σ (- x) = 1$