Q learning 學習筆記本
簡介⌗
什麼是強化學習⌗

強化學習是機器學習的其中一個分支,介於監督式學習與非監督式學習之間,在與環境互動的過程中你不會馬上知道你做的是對或錯也無法知道環境會怎麼變化,等到一定的時間延遲後才會明瞭,通過試錯把利益或獎勵極大化。有沒有看過明日邊界 (Edge of Tomorrow) 這部電影?劇中主角凱吉經過一次一次試錯、死亡,經驗值漸漸累積慢慢變強,這就是強化學習。
強化學習的元件⌗
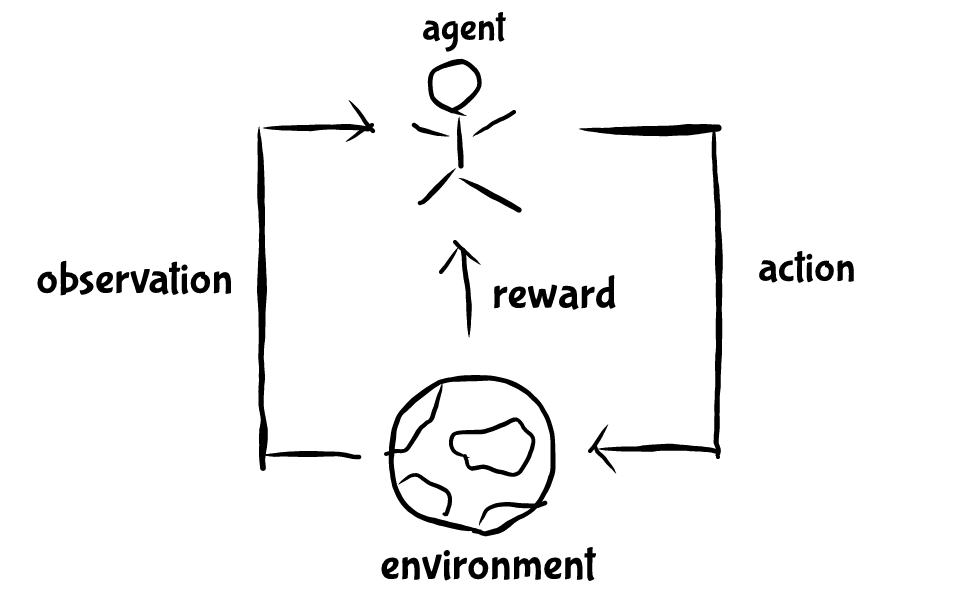
更正式一點來說,要學習的主體我們稱為機器人 (agent),機器人做出動作 (action) 跟環境 (environment) 互動,環境反饋獎勵 (reward) 給機器人,這時機器人再藉由獎勵和接下來的環境判斷接下來該做什麼動作,所以重點就在機器人 怎麼判斷,通常會從歷史中累積經驗,經驗這個東西更準確地來說就是你記得的事。再往下講得更複雜之前先跳脫一下來問個小問題,假如你是一隻小老鼠,有個拉把你可以,第一次旁邊的燈泡亮了兩下然後你拉了一下拉把,接下來鈴鐺想了一下,然後你就被電了,第二次鈴鐺響了一下,燈亮了一下,你拉了兩下拉把,突然你就獲得一塊小起司,第三次你拉了一下拉把,燈泡亮了一下,你又拉了一下拉把,燈泡亮了一下,你覺得你現在會被電還是獲得起司?
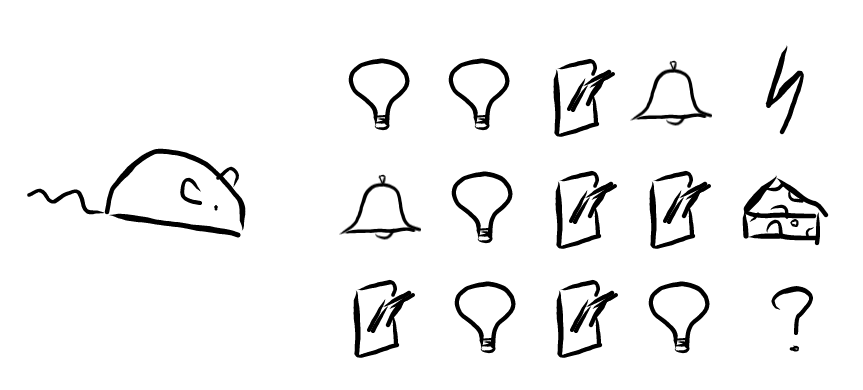
如果你覺得起司和電擊是取決於你拉把的次數,那這次你應該就會覺得你會獲得起司了;但如果你覺得是取決於燈泡的數量,那你可能會覺得你會被電。所以你怎麼看待你的經驗很重要,會決定你接下來的選擇(跟阿德勒心理學好像啊),我們平常也是用以前經驗和經驗的好壞決定以後的選擇,用制式一點的說法就是把發生過的事稱為狀態 (state),機器人的目標就是用狀態和獎勵決定接下來的動作最大化總獎勵,機器人會有自己表達狀態的方式,環境也有自己的狀態,但機器人不會知道,也跟機器人要怎麼做決定無關,所以接下來我們提到的狀態指的都是機器人狀態。 那機器人會如何做決定呢?通常機器人會依靠以下其中一到三個重要的元件做決定:
- 模型 (model):這個機器人表達環境的方式
- 價值函數 (value function):評估一個動作或狀態好壞的函數
- 策略 (policy):決定機器人行為的函數
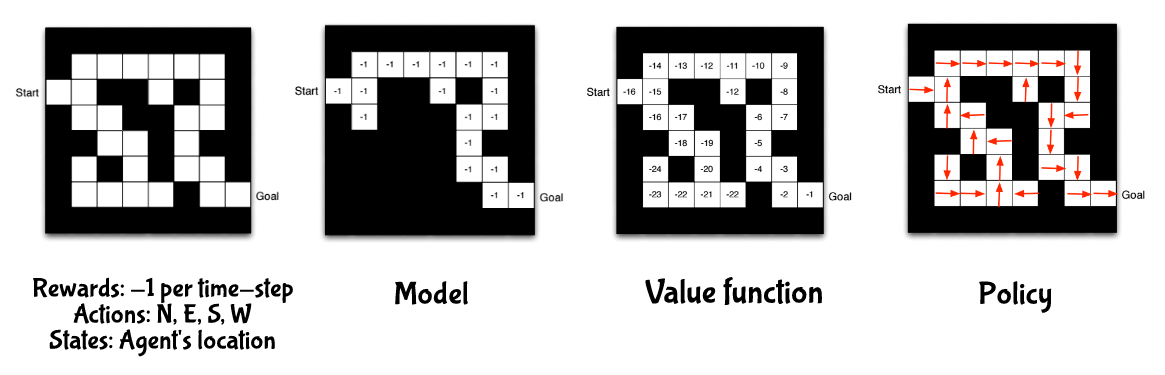
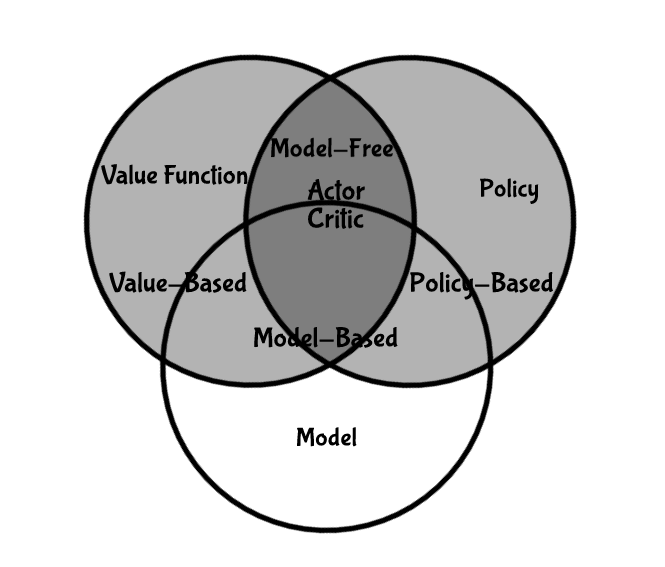
舉個例子,一個迷宮遊戲,越快走到終點越好,所以獎勵是每走一步就 -1 ,你有東西南北這四個選項可以選,狀態用機器人的位置來表示,對於這個遊戲而言,模型是在機器人心中對整個環境的描述,會因為它走不同的路而有不同的模型,上圖左二就是其中一個模型,白色的地方表示他走過的路,裡面的數字代表他知道走過獲得的獎勵,上圖左三每個白格中的數值是每個狀態的價值,用來判斷這個狀態的好壞,上圖左四中的箭頭代表每個狀態的策略。所以所有強化學習的演算法都可以用這三個元素來分類,如下圖(不存在只有模型的強化學習演算法)。
馬可夫⌗
馬可夫過程⌗


我們需要更正式一點定義每個狀態轉換的表達方式,剛好有一個很有用的工具可以用來表達,就是馬可夫鏈,馬可夫鏈是滿足馬可夫性質的隨機過程,那什麼是馬可夫性質?如果一個狀態轉換到下一個狀態的機率分佈只跟當前狀態有關,就符合馬可夫性質,講白一點就是未來跟過去沒關係,只跟現在有關係,因為現在是由過去組成的,跟強化學習所面對的問題是一致的,舉個例子
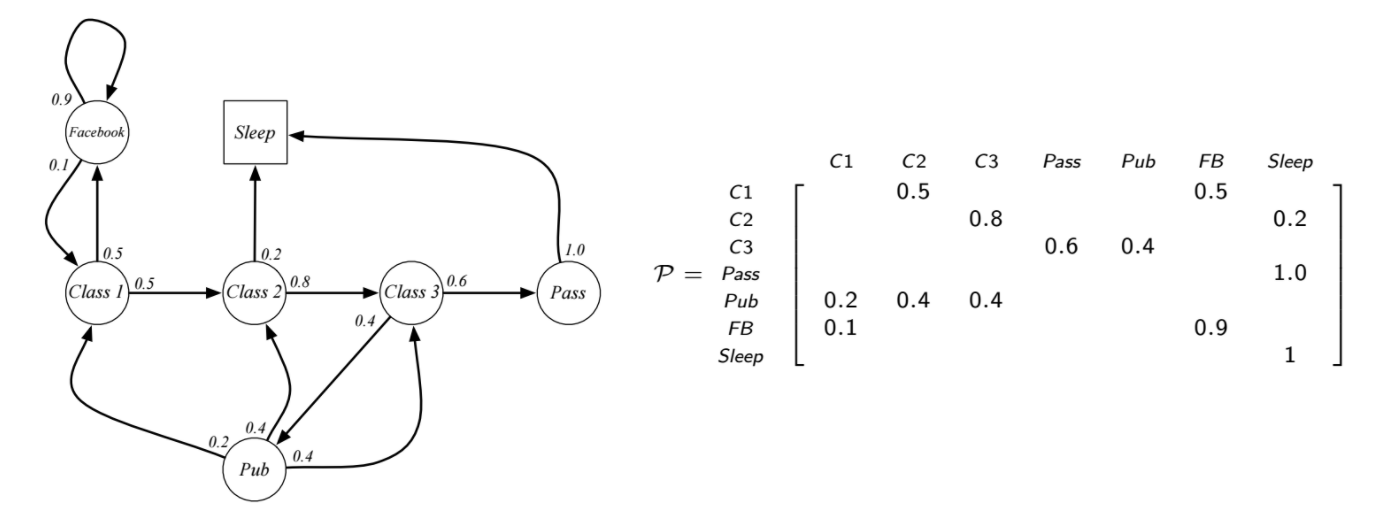
上圖左是一個學生馬可夫鏈,學生在不同的狀態都有機會轉移到不同狀態(這裡先假定學生自己沒選擇權),每個狀態旁邊的數字是轉移機率,定義 class1 是初始狀態,睡覺 (sleep) 是最終狀態,因為他不會再轉移到別的狀態,上圖右就是這個馬可夫鏈的轉移機率矩陣,一個回合 (episode) 有可能是 class1 -> class2 -> class3 -> pass -> sleep,或是 class1 -> class2 -> pub -> class1 -> class2 -> class3 -> pass -> sleep,接下來我們加上有獎勵的馬可夫鏈
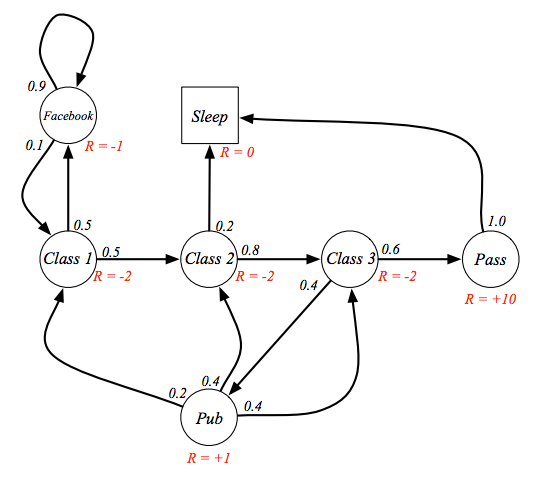
馬可夫獎勵過程⌗
這時可以讓機器人知道在哪個狀態是比較好的了嗎?還不能,因為他只知道在某個狀態底下的獎勵是什麼,無法有個宏觀的角度看待,就像是讀書對我們來說很累當下的獎勵應該超級低甚至是負的,但因為我們知道讀書對未來的報酬率很高所以會願意花時間,那在馬可夫鏈中該如何表示呢?引入一個觀念:報酬 (return),如下圖,報酬由獎勵累加而成,但越遠的動作或狀態可能越不重要,所以每個獎勵都乘上一個衰減因子 (discount factor),衰減因子介於 0 到 1 之間,如果是 0 代表非常短視近利,只看前一步的獎勵,如果 1 代表非常深謀遠慮,把每一步的獎勵都看成相同的價值,有了衰減因子和獎勵的概念後,就可以把馬可夫過程增加變成馬可夫獎勵過程,如下圖二。


這時我們就可以定義每個狀態的好壞了,可以用一個狀態價值函數來表示,狀態價值函數就是輸入某個狀態輸出如果從那個狀態開始走的馬可夫獎勵過程報酬期望值,用剛才讀書的例子,因為你的爸媽告訴你讀書的報酬率很高可能可以賺大錢,耍廢對未來報酬率不高,所以在你心中的狀態價值函數讀書這個狀態的價值高,雖然當下的獎勵是負的,耍廢這個狀態的價值低,雖然當下的獎勵是很高的,假設你是理性的話你就會在當下選擇讀書。

可以把狀態價值函數改寫一下,變成由兩個部分組成,第一個部分是當下的獎勵,加上第二部分是未來一個狀態的狀態價值函數值乘上衰減因子,這就是貝爾曼方程式。
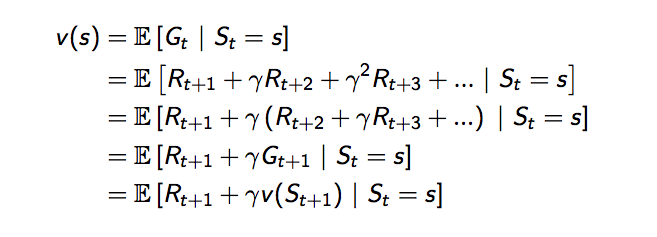
再改寫一下,用示意圖來看看,白色圓圈代表每個狀態,時間軸由上而下,根據期望值的定義狀態價值函數可以寫成,當下獎勵加上加總的未來狀態價值乘上發生這個狀態的機率再乘上衰減因子
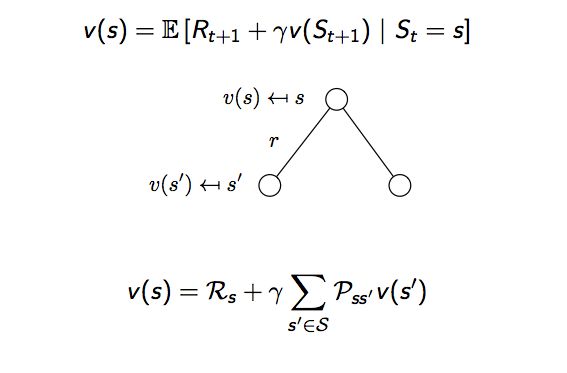
實際算算看,回到剛剛學生馬可夫鏈的例子,設定衰減因子是 1,以 class3 這個狀態為例,當下的獎勵是 -2,加上有 0.6 的機率到達 pass 這個狀態,它的獎勵是 10,有 0.4 的機率到 pub ,獎勵是 0.8,所以 class3 的價值就是 4.3,其實也可以由此看出這個貝爾曼方程式是線性方程式,可以直接解。
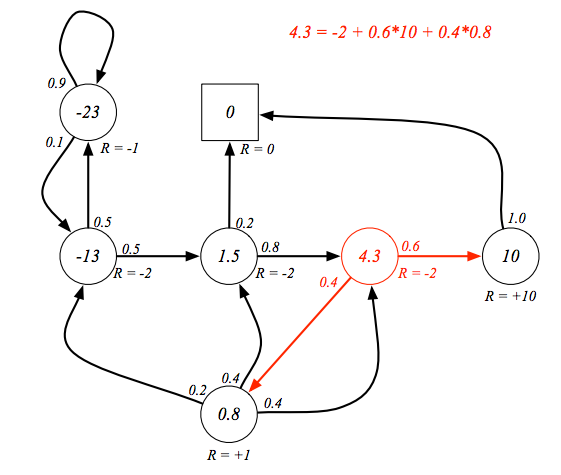
這時我們該加入動作這個觀念了。
馬可夫決策過程⌗

剛剛學生馬可夫的例子,並沒有讓學生有選擇權,不太合理,所以改寫一下,這時學生有自由意志可以選擇他想到哪個狀態,除了去 pub,去了 pub 之後環境有 0.2 的機率讓學生轉移到 class1 的狀態,也有各 0.4 的機率轉移到 class2 或 class3。
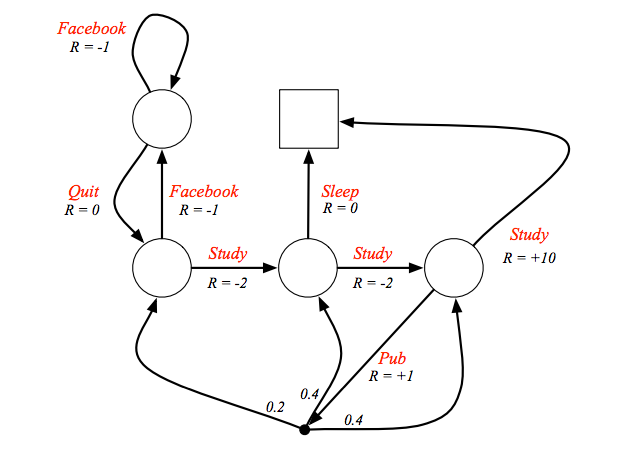
這時學生要怎麼選擇就由策略決定了,策略是給定當下狀態選擇某個動作的的機率函數。

那就可以再把價值函數改寫了,前面所講的價值函數都是狀態價值函數,可以改寫成在某個策略下的狀態價值函數,因為有可能因為不同策略而有不同的狀態價值,另外很重要的是現在我們可以有動作價值函數了,也就是俗稱的 q 值,動作價值函數是在某個策略某個狀態某個狀態下做某個動作的期望報酬,跟原本的狀態價值函數幾乎一樣,差別只在多了動作的概念,有了 q 值我們才能評斷做這個動作到底好不好

跟狀態價值函數可以分成兩個部分,動作價值函數也可以分成當下做這個動作的獎勵,加上未來可能做的動作的動作價值乘上衰減因子
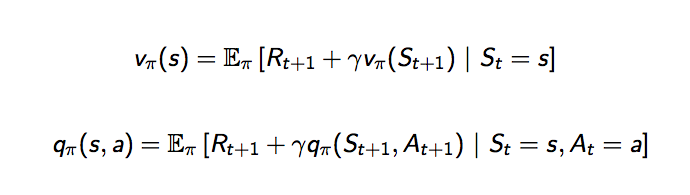
再用示意圖來解釋,白點代表狀態,黑點代表選擇的動作,時間軸一樣從上到下,下圖左,一個狀態的價值可以相等於接下來可能會做的動作的動作價值函數加總,下圖右,一個動作的價值可以相等於做這個動作的當下獎勵加上所有可能發生的狀態的價值加總
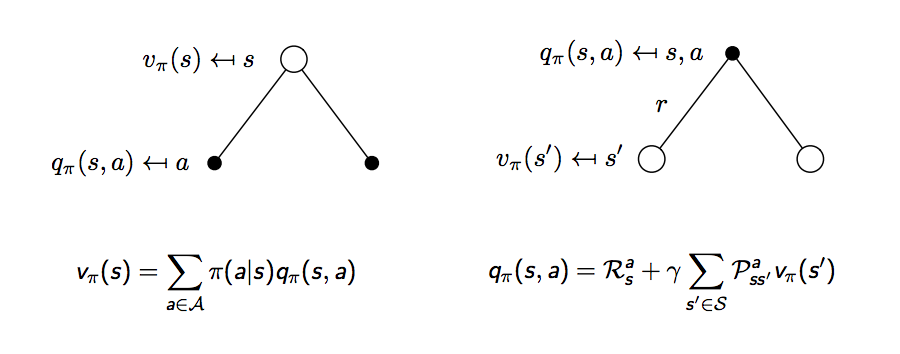
但這怎麼跟上面的式子不太一樣?因為上面的式子寫的是狀態價值函數相對狀態價值函數,動作價值函數相對動作價值函數,所以還要再擴展一步,下圖這兩個公式也稱為對狀態價值函數的貝爾曼期望等式 (Bellman expectation equation) 和對動作價值函數的貝爾曼期望等式
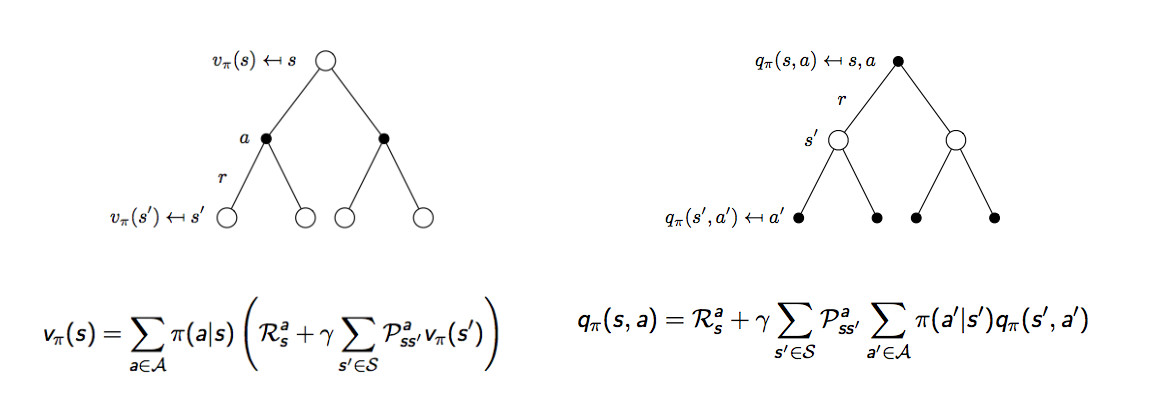
舉個例子,上面圖左假設你現在在玩寶可夢,你在最上面那個白點,狀態是你發現你隔壁巷子現在有一隻卡比獸出沒,接下來你有兩個選擇,一個是跑去隔壁巷子,另外一個選擇是待在原地等看看還有沒有其他寶可夢,這兩個動作分別用不同的黑點代表,所以白點到黑點的路徑你可以選擇,做哪個決定的機率取決於策略,這時如果你選擇跑到隔壁巷子,有可能你順利抓到卡比獸,也有可能卡比獸消失了,如果你選擇待在原地,有可能突然就出現乘龍,也有可能沒半點寶可夢出現,所以黑點到哪個白點是環境給的,機器人或玩家無法決定,回到剛剛學生馬可夫的例子,來計算看看
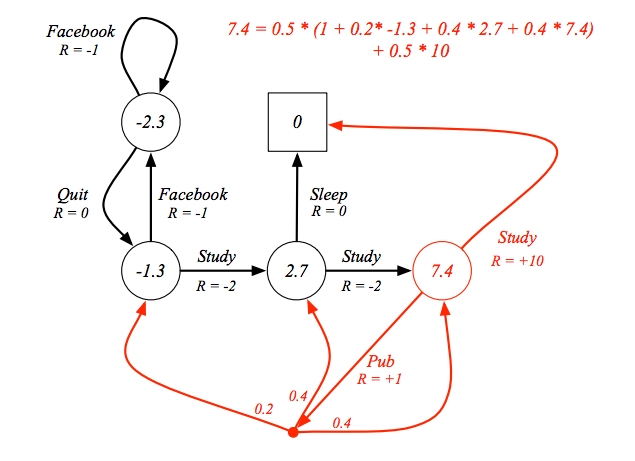
假設設定策略是隨機,也就是做什麼動作的機率都一樣,如果有兩個動作可以選,選任一的機率就是 0.5,以 class3 這個狀態為例,有 0.5 的機率選擇 study,study 這個動作的獎勵是 10,study 後只會有一個結果就是到達終點這個狀態而且沒有獎勵,所以選擇這個動作的價值就是 0.5 x 10,另外有 0.5 的機率去 pub,選擇 pub 這個動作馬上有 1 的獎勵,選擇去 pub 接下來有三個可能的結果,有 0.2 的機率到達 class1,class1 的狀態價值是 -1.3,有 0.4 的機率到 class2,狀態價值是 2.7,也有 0.4 的機率回到 class3,所以就能算出 class3 這個狀態價值是多少,有可能有人會有疑惑我明明想算 class3 的狀態價值但為什麼在等式中已經有 class3 的狀態價值了,因為其實正確算法應該是把所有的等式列出來,再解線性方程式,這裡只是為了方便講解所以把其中一個等式拉出來講
最佳化馬可夫決策過程⌗
既然有了每個動作的價值,每個狀態的價值,再來不就找出最好的就結束了嗎?對,所以我們先定義,最佳的狀態價值函數就是所有策略下能夠有最大值的那個策略下的狀態價值函數,同樣最佳的動作價值函數是產生最大值動作價值策略下的動作價值函數

以學生馬可夫為例,下圖左為衰減因子為 1 時的最佳狀態價值函數,下圖右是衰減因子為 1 時的最佳動作價值函數
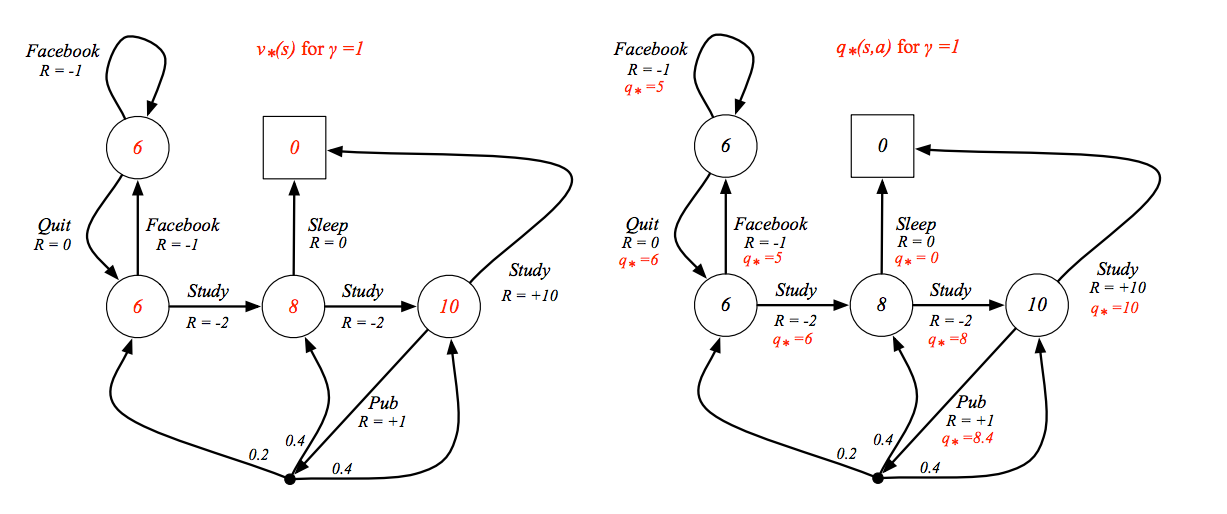
這時就會發現,如果你已經知道最佳的動作價值函數,只要照著最好的動作走,這就會是最佳的策略,如下圖紅色的路徑
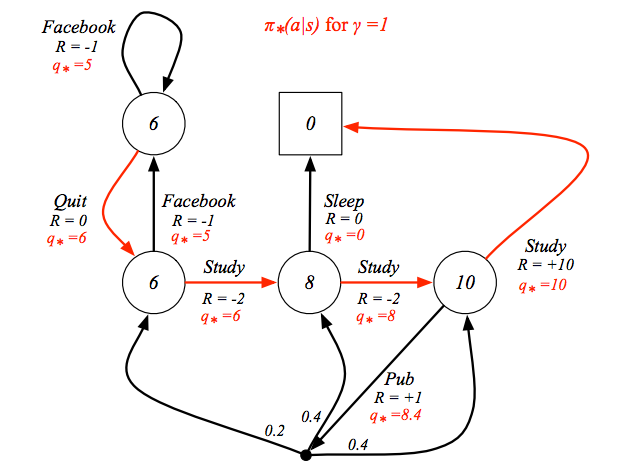
回到剛剛的黑白點示意圖,價值函數要用最大的動作價值函數值去計算
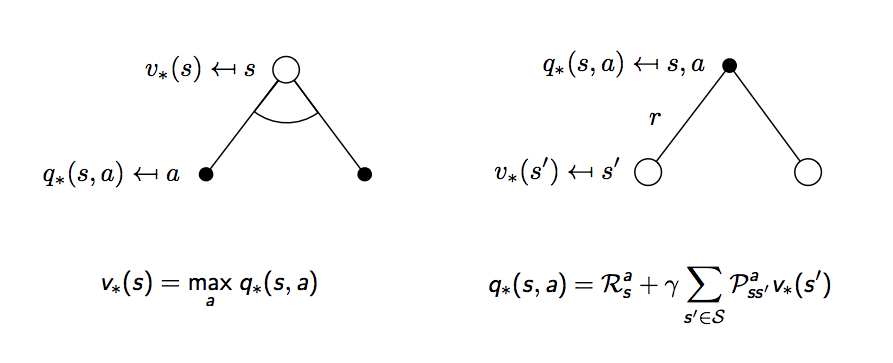
同樣也要再擴展一步
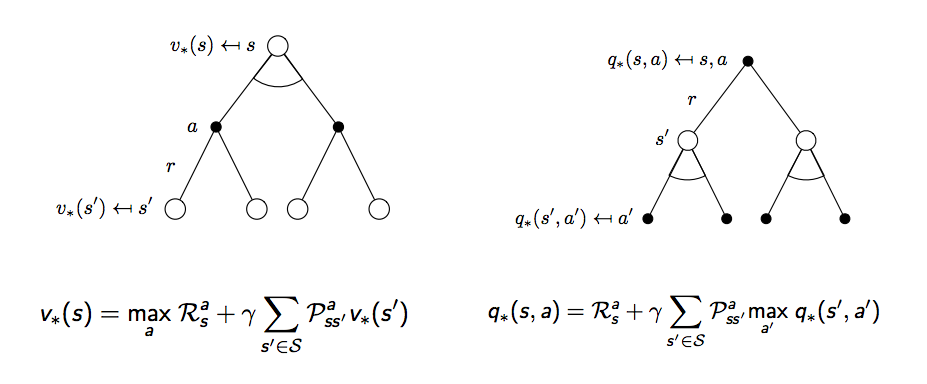
上圖這兩個公式也稱為對狀態價值函數的貝爾曼最佳等式 (Bellman optimality equation) 和對動作價值函數的貝爾曼最佳等式,至此我們要解的問題就已成形,但這時不像前面都是線性方程式,需要用迭代的方式去把最佳解找出來,接下來會講到四種解法
- 策略迭代 (policy iteration)
- 價值迭代 (value iteration)
- SARSA
- Q Learning
策略迭代與價值迭代⌗
我們先回到沒有選擇可以做什麼動作的設定,等到講解完沒有動作 (也就是只有 v 值,沒有 q 值的設定) 後再來討論 q 值。剛整理出狀態價值函數有兩個貝爾曼等式,先看貝爾曼期望等式,雖然在前面說這個可以用線性方程式解,但當整個馬可夫鏈變得非常龐大時就會變得很複雜,比較好的方式是一次一次迭代讓 v 值收斂,等 v 值收斂後再改善策略,如何改善?用貪婪方式改善策略,也就是總是找目前看到最好的,如果有點難懂可以看下圖
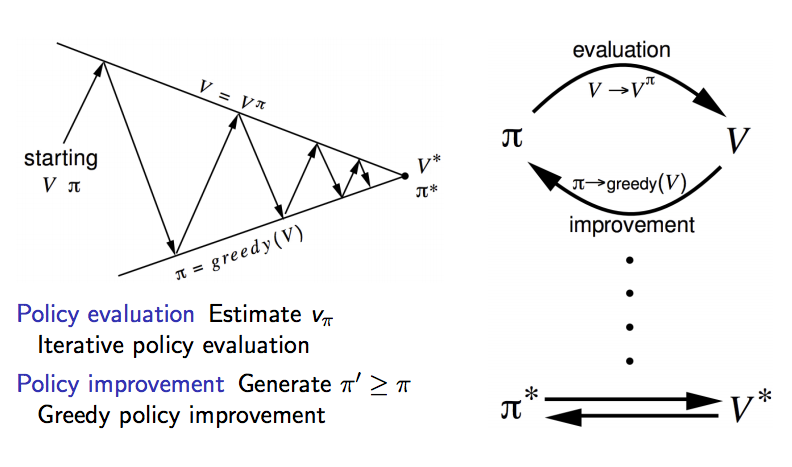
先固定一個策略,讓機器人一次一次的探索更新每個狀態的價值,到達收斂後,用貪婪算法更新策略,再次讓機器人收斂 v 值,重複不斷下去,這個解法就叫做策略迭代,相信這樣大家應該還是不太懂,舉個例子
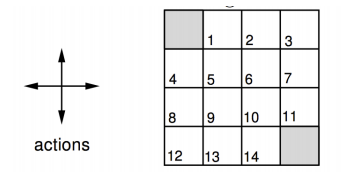
在這個 4 x 4 的小格子世界中,任務是花最少步數走到終點,終點在左上和右下角,每走一步的獎勵是 -1,有上下左右四個動作可以選擇,一開始遵行上下左右選擇的機率都是 0.25 的策略
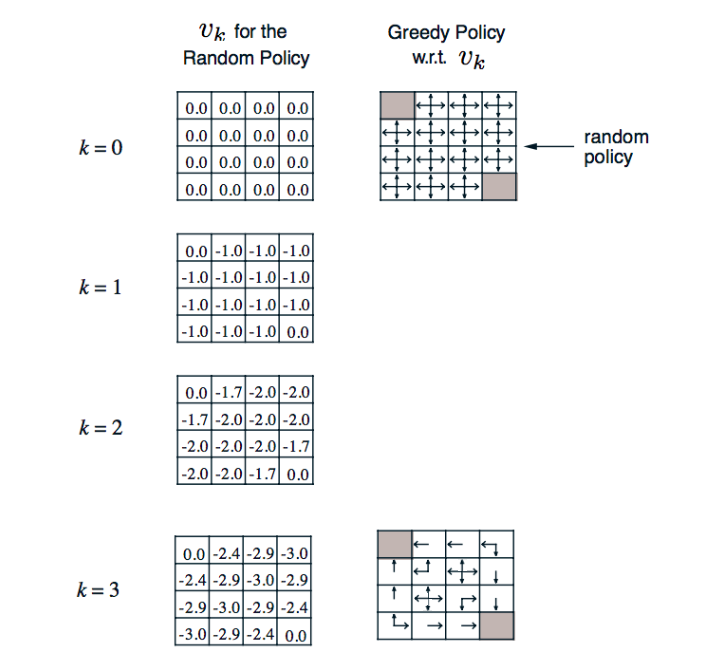
k 代表第幾輪,左欄代表在不同輪時的狀態價值,也就是 v 值,第零輪因為都沒走過所以每個格子都是 0,第一輪,以上左二格子為例,當下獎勵是 -1,加上未來可能 v 值為 0 x 0.25 + 0 x 0.25 + 0 x 0.25 + 0 x 0.25 (往上走沒有路,所以計算留在這格的價值),所以這兩部分相加就是 -1,以此類推這輪的其他格,第二輪,一樣以上左二格子為例,當下獎勵是 -1,未來可能 v 值 0 x 0.25 + -1 x 0.25 + -1 x 0.25 + -1 x 0.25,兩部份相加是 -1.75 (圖中因為空間關係無條件捨去小數點第二位),後面幾輪以此類推;右欄箭頭表示策略,一開始用隨機的策略,到達第三輪時用貪婪方式更新策略。由於貪婪方法就是選擇當下最好的,那為何不把這個想法直接放在更新 v 值時使用呢?沒錯,就直接用貝爾曼最佳等式不就好了,沒有明確用哪個策略,直接更新貝爾曼最佳等式這種方式就叫做價值迭代,可以看一下兩個的比較
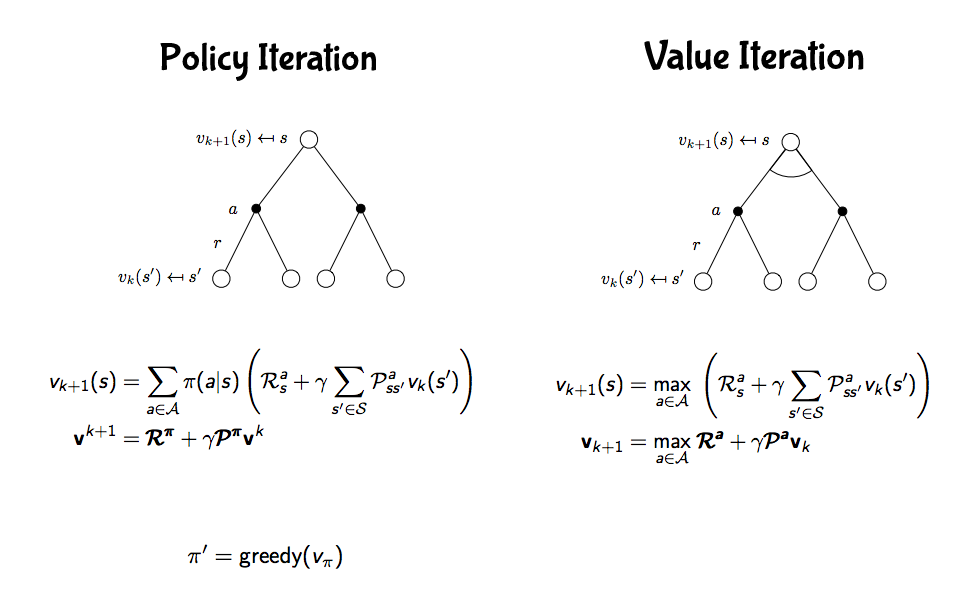
用剛剛的小格子世界來比較兩種的 v 值如下圖

這兩種方式是動態規劃的一種方式,所以可以統稱動態規劃更新方式,到這感覺應該結束了,但有沒有發現這兩種方式都要把所有路徑都走完,才能正確得知道在哪個狀態下要怎麼走,這兩種方式更新 v 值的方式我們稱為全域的更新 (full-width backup),需要知道這個馬可夫鏈的所有轉移機率和獎勵,當馬可夫鏈變得越來越龐大時越來越不可行,我們需要別的方法。
Q Learning 與 SARSA⌗
蒙地卡羅⌗
既然全域的更新方式看似完美但不太可行,那我們就用抽樣的更新 (sample backup) 方式好了,不需要知道整個馬可夫鏈,有走過的路更新就好,沒走過就算了吧,從經驗中學習,當完成一回合時就更新所有走過狀態的值,那該怎麼更新呢?前面提過的更新方式是用報酬期望值,但在這裡因為我們不知道發生不同狀態的機率,所以無法用期望值,那最簡單的想法就是用平均報酬好了,經過很多次回合後平均這個狀態的報酬就是這個狀態的狀態價值,這種方式就稱為蒙地卡羅 (Monte-Carlo),
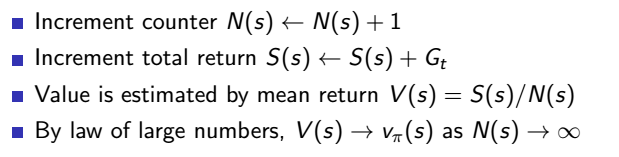
改寫一下公式,得知這樣的平均值可以用每次累計 (incremental) 的方式計算,也就是我們的機器人每走一回合就可以算一次平均,不用等到所有回合都結束後再算
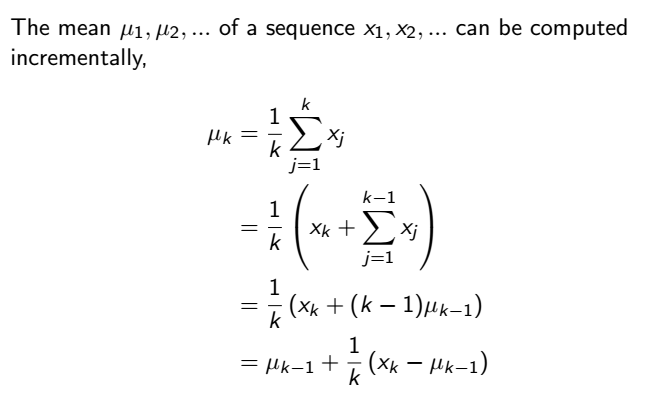
那就可以再改寫蒙地卡羅更新方式,如下
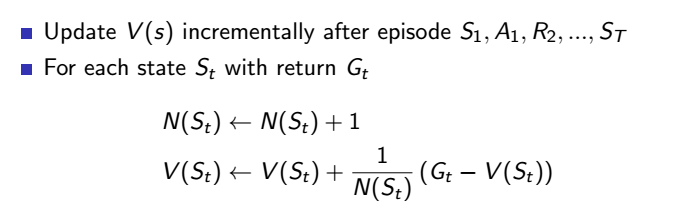
可以看到這個公式中除以總次數的這個值,我們可以把它用 alpha 代替,變成一個可調整的參數,alpha 可介於 0 到 1 之間,0 代表不要參考這次回合的結果,1 代表很看重這次回合的結果,藉此可調整對新經驗的看重
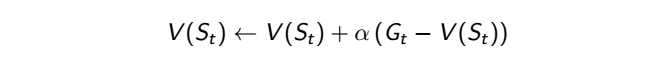
時間分差⌗
用蒙地卡羅方法需要等每個回合結束後才能更新,這樣有點慢,而且如果這個遊戲是沒有回合的,像是人生只能過一次,那你不就永遠沒辦法更新變強?所以最好的方式就是往後走幾步就更新 v 值,這樣就不用等一個回合結束後才更新,這種方式就叫做時間分差 (temporal-difference)。

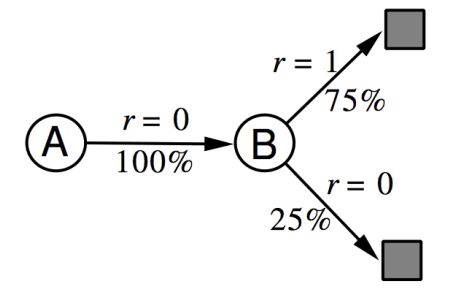
原本用總報酬更新的方式改成只看下一步,只看公式可能不太懂,再來舉個例子,下圖是一個小遊戲,有 A、B 兩種狀態,你經過 8 個回合,經過的狀態和獎勵分別如下,設定 alpha 值都為 1,這時你覺得 A、B 狀態價值分別為多少?註:我這裡沒有用迭代的方式算,因為是個只有 8 回合的小遊戲,用迭代的方式算出來會是一樣的結果

蒙地卡羅法 A:0 B:6 / 8 = 0.75
時間分差法 可以在內心先畫出目前探索出來的馬可夫鏈,如下圖 A:0.75 * 1 + 0.25 * 0 = 0.75 B:6 / 8 = 0.75
總結一下剛講到的幾種方式
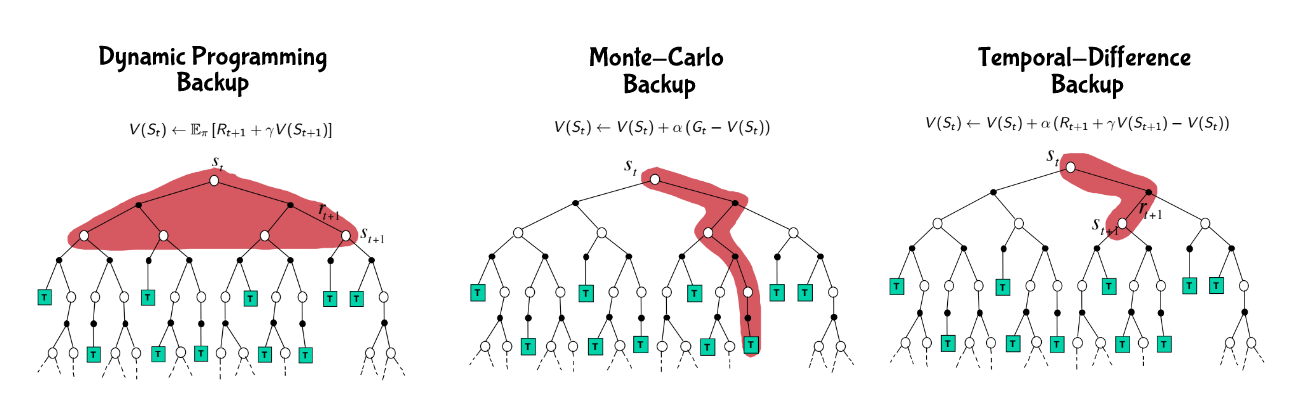
如果用一個光譜來看的話就像這樣
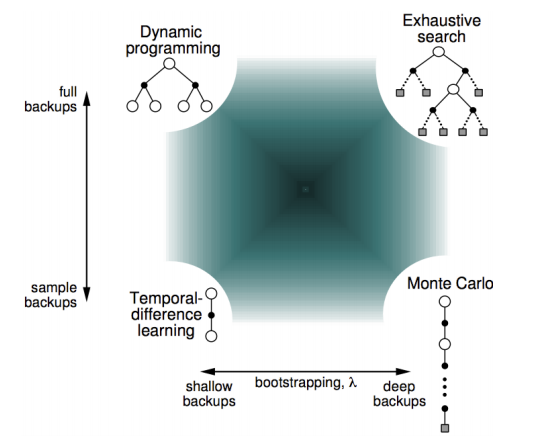
SARSA⌗
接下來終於可以把動作加進去了,所以從原本的狀態價值更新改成動作價值更新
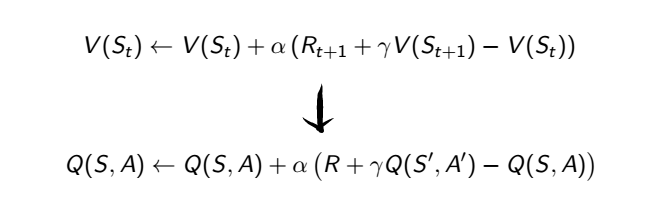
這種迭代方式就叫做 SARSA,為什麼叫 SARSA 呢?因為就是 S・A・R・S・A
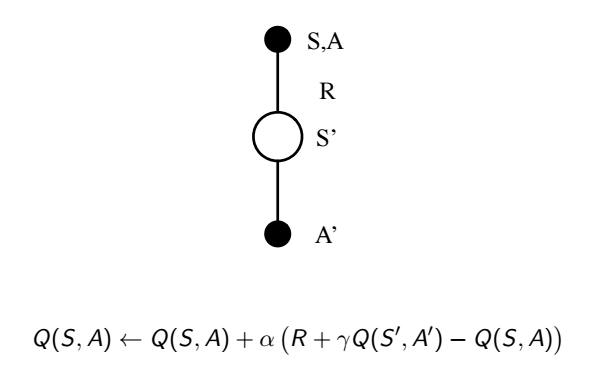
SARSA 需要先確定某個策略,收斂 q 值後再更新策略,持續收斂,這種方式稱為跟隨策略 (on-policy) 的方式,值得一提的是,剛才提到策略都是貪婪式策略,但太貪婪的下場會不會失去更好的機會?舉個例子,假如你是個很聰明學什麼都很快的人,小時候爸媽就讓你念數學,你的數學成績也是所有科目裡最好的,所以你就一直唸數學唸下去,但說不定其實你藝術細胞也不錯,只是因為你一直選擇唸數學,所以沒機會知道自己還有別的潛能,這樣該怎麼辦?要增加一些探索未知領域的機會,這裡稱為 epsilon 貪婪策略 (epsilon-greedy)

有 epsilon 的機率你可以隨機亂選動作,1 - epsilon 的機率用貪婪策略,以下是 SARSA 的演算法

Q Learning⌗
跟前面策略迭代到價值迭代的思維一樣,既然我每次都要等 q 值收斂後才能用貪婪方式更新策略,為何我不能直接把貪婪的想法直接放入更新 q 值中?可以,誕生新的演算法,這個方式就是赫赫有名的 q learning,這種方式也是一種不跟隨策略 (off-policy) 的方式
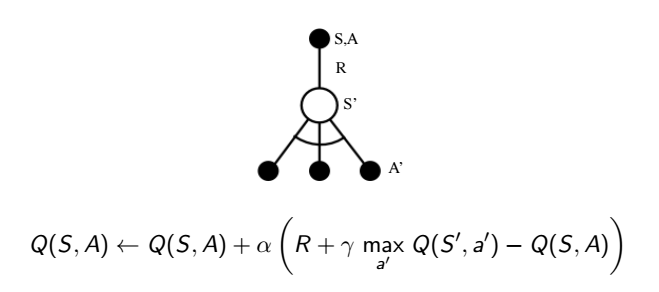
以下是 q learning 的演算法 (其實跟 SARSA 真的只差在更新的公式)

總結⌗
前面所講的演算法可用兩張圖總結
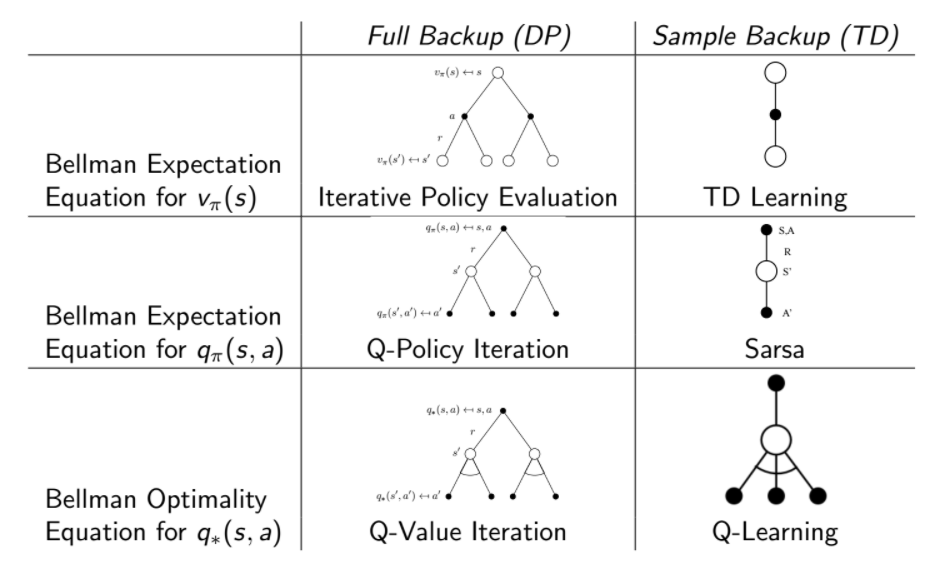
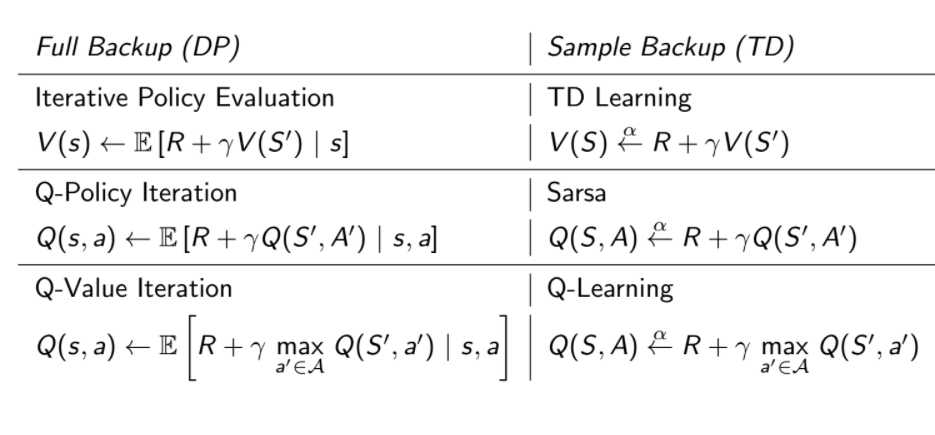
專有名詞對照表⌗
- agent 機器人
- environment 環境
- reward 獎勵
- state 狀態
- action 動作
- model 模型
- value function 價值函數
- policy 策略
- episode 回合
- return 報酬
- discount factor 衰減因子
- Bellman expectation equation 貝爾曼期望等式
- Bellman optimality equation 貝爾曼最佳等式
- policy iteration 策略迭代
- value iteration 價值迭代
- full-width backup 全域更新
- sample backup 抽樣更新
- Monte-Carlo 蒙地卡羅
- temporal-difference 時間分差
- on-policy 跟隨策略
- off-policy 不跟隨策略